一.递归法实现二叉树遍历
前序遍历
创建一个节点类 属性是val,左节点,右节点
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}前序遍历
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<Integer>();
preorder(root, result);
return result;
}
public void preorder(TreeNode root, List<Integer> result) {
if (root == null) {
return;
}
result.add(root.val);//中
preorder(root.left, result);//递归遍历左子树
preorder(root.right, result);//递归遍历右子树
}
}中序遍历
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
inorder(root, res);
return res;
}
void inorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
inorder(root.left, list);//递归遍历左子树
list.add(root.val); //中 加入集合
inorder(root.right, list);//递归遍历右子树
}
}后序遍历
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
postorder(root, res);
return res;
}
void postorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
postorder(root.left, list);//递归遍历左子树
postorder(root.right, list);//递归遍历右子树
list.add(root.val); //处理中间结点
}
}二.迭代法实现
迭代法就是用栈结构模拟递归法的压栈出栈操作,实现对二叉树的前序后序中序遍历
1.前序遍历迭代法实现
前序遍历:中右左->中左右
中节点先加入结果res,然后先右后左入栈,出栈时先左后右,加入res,组成中左右
如果只有3个节点二叉树
中节点先进入栈,中节点弹出,中节点加入res,
中节点右孩子入栈,中节点左孩子入栈,此时栈里面是右左,数组里面只有一个中,出栈顺序就是左右,
出栈依次处理完毕加入数组就是中左右
举例说明

代码实现
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null){
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.pop();
result.add(node.val);//处理中
if (node.right != null){
stack.push(node.right);
//先加入右再加入左,确保出栈时先左后右的前序遍历
}
if (node.left != null){
stack.push(node.left);
}
}
return result;
}
}2.后序遍历迭代法实现
前序遍历程序顺序是中右左,结果集合是中左右:
前序遍历:中右左->中左右
如果把前序遍历程序中右左的左右颠倒 得到程序中左右
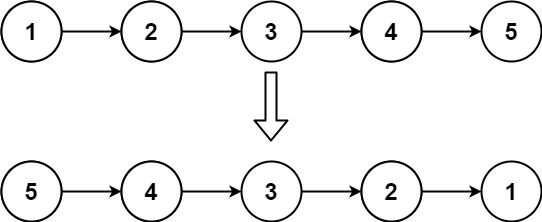
此时中左右此时结果集合应该是中右左
再对结果翻转得到左右中即为后序遍历
代码实现
// 后序遍历顺序 左-右-中 入栈顺序:中-左-右 出栈顺序:中-右-左, 最后翻转结果
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null){
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.pop();
result.add(node.val);
if (node.left != null){
stack.push(node.left);
}
if (node.right != null){
stack.push(node.right);
}
}
Collections.reverse(result);
return result;
}
}3.中序遍历迭代法实现
中序遍历的顺序是左中右
但是我们一开始遍历起点是中,所以我们要从中结点开始不断找左孩子,在这个过程中保存经过的值(必然是使用栈保存,先进后出)
元素为空时,回退,从栈里面弹出元素,向右走一步,
元素不为空时,元素入栈,向左走
具体分析如下

代码实现
// 中序遍历顺序: 左-中-右 入栈顺序: 左-右
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null){
return result;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()){
if (cur != null){
stack.push(cur);
cur = cur.left;
}else{
cur = stack.pop();
result.add(cur.val);
cur = cur.right;
}
}
return result;
}
}三.递归法迭代法总结
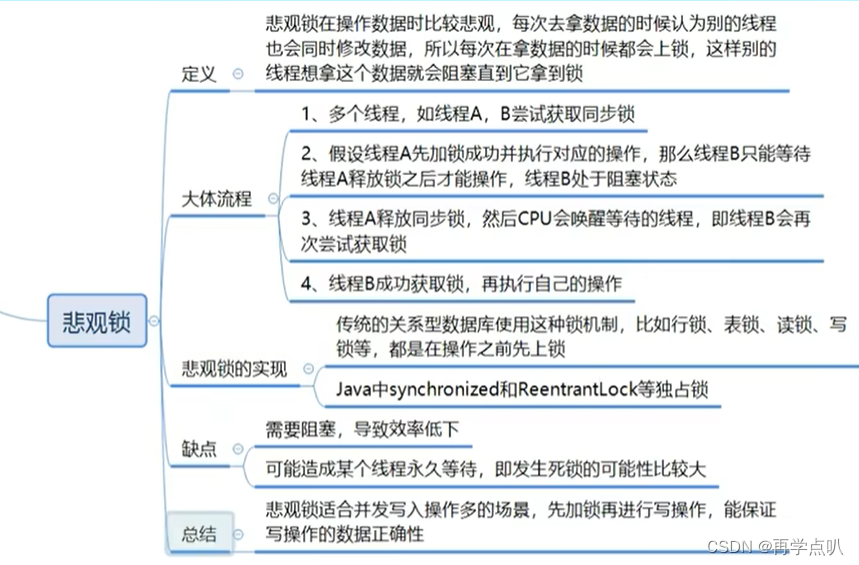
递归法和迭代法都可以实现对二叉树的遍历,但它们在实现方式、内存消耗和适用场景等方面存在差异。
递归法直观易懂,但可能受到栈空间的限制;
迭代法实现相对复杂,但更加高效且稳定。
在实际应用中,可以根据具体需求和场景选择合适的方法。